最优化方法——梯度下降法、牛顿法、LM算法

介绍： 在机器学习中应用十分的广泛，主要目的是通过迭代的方式找到目标函数的最小值（极小值）。其基本思想是：以所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处。

梯度: 在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率
在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向。下面举个例子：

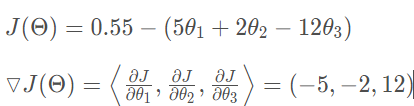
数学表示:

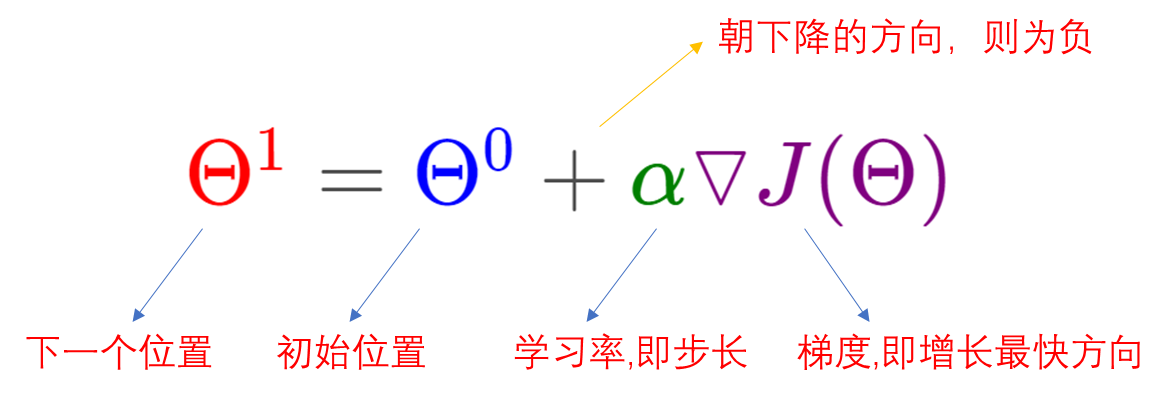
笔者注： 最优化方法最核心是求解目标函数的极值点（最大值、最小值点），可以通过建立一个代价函数，将该问题转变寻找最合适的曲线拟合点的问题（此时代价函数的极值点即为该曲线的参数）。方法如下：

参考文章：https://blog.csdn.net/qq_41800366/article/details/86583789

介绍： 牛顿法是求解无约束优化问题最早使用的经典方法之一，其基本思想是：用迭代点$x_k$处的一阶导数（梯度）和二阶导数（Hesse阵）对目标函数进行二次函数近似，然后把二次模型的极小值点作为新的迭代点，并不断重复这一过程，直至求得满足精确度的近似极小值点。

参考视频：https://www.bilibili.com/video/BV1AF411z7hg/?spm_id_from=333.788.recommend_more_video.1

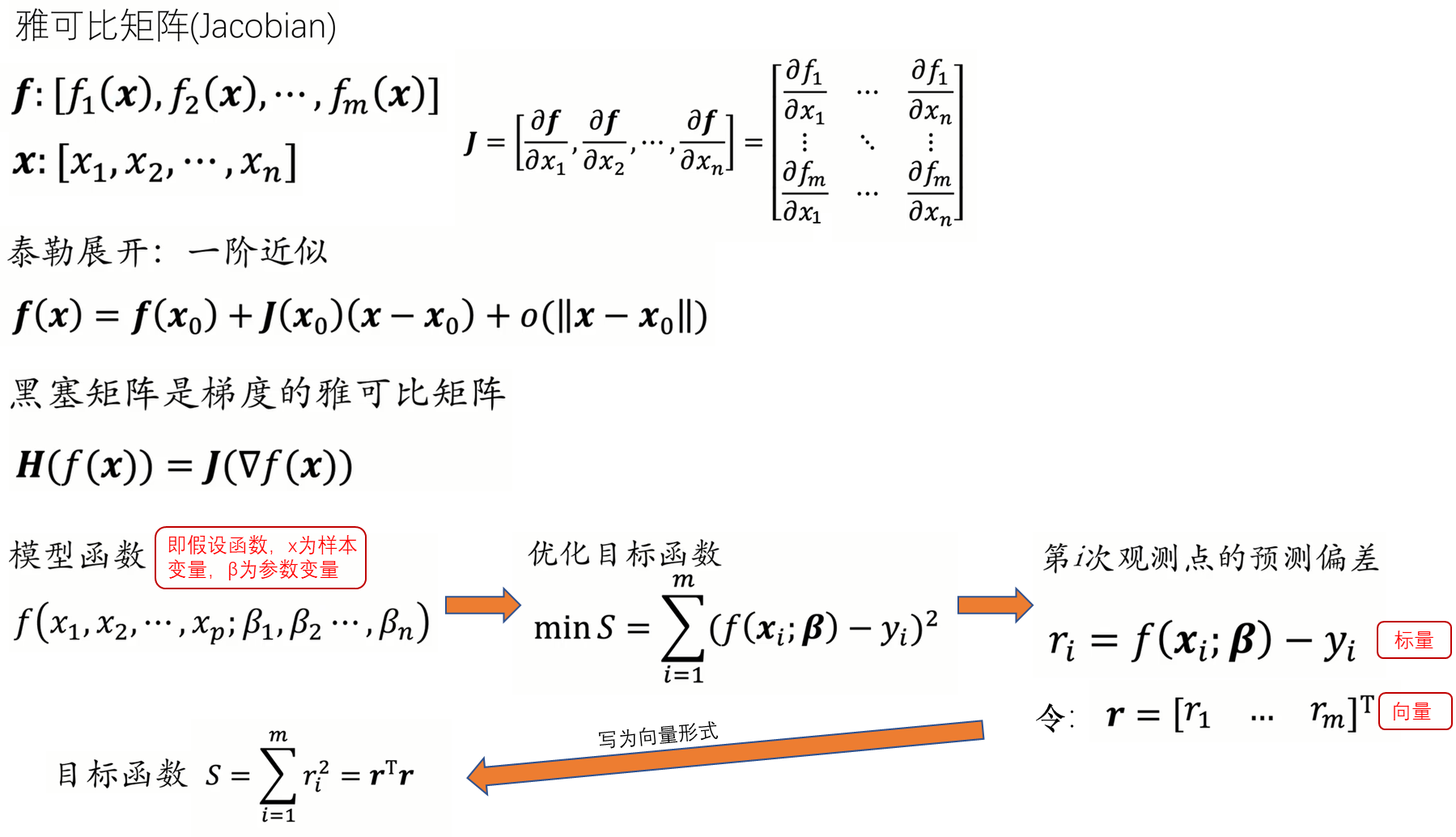
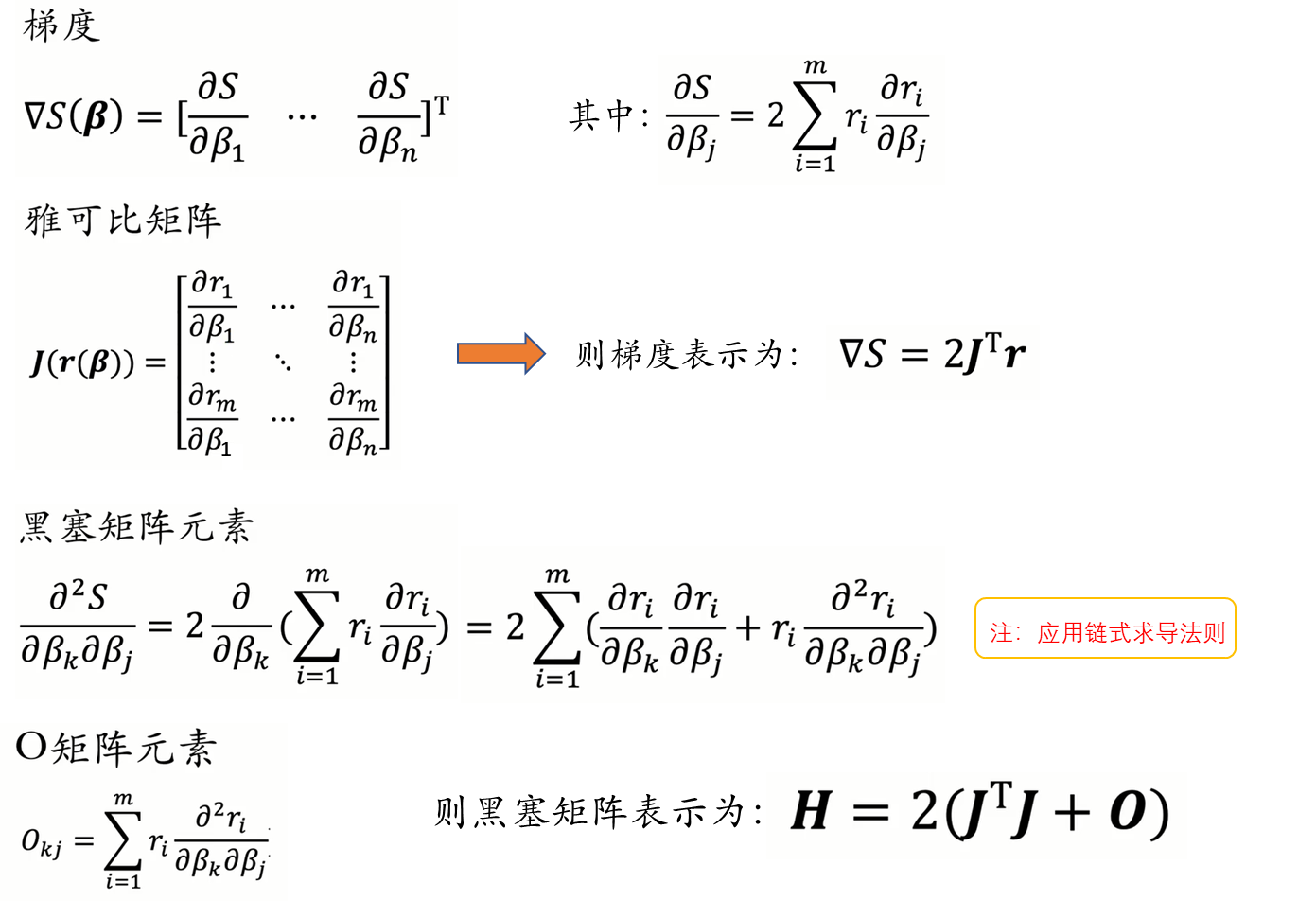
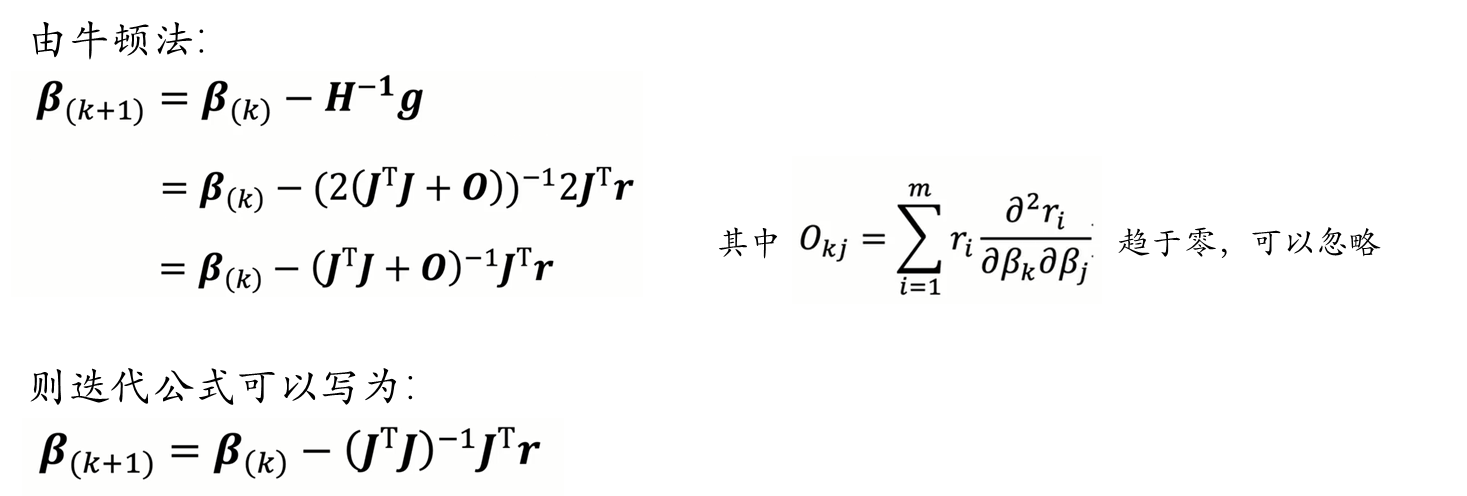
牛顿法虽然收敛速度快，但是需要计算黑塞矩阵（Hessian matrix），对于高维的问题，计算二阶导数会很复杂。因此我们有了Gauss-Newton算法。Gauss-Newton算法不直接计算黑塞矩阵（Hessian matrix），而是通过雅各比矩阵（Jacobian matrix ） 对 黑塞矩阵（Hessian matrix） 进行拟合：
$$H\approx J^{T}J$$
但是，用 雅各比矩阵（Jacobian matrix ）拟合黑塞矩阵（Hessian matrix），所计算出来的结果不一定是正定的，即无法保证下降，所以要引入一个对角矩阵与之相加（如果有特征值为负，加上$\mu$后就修正为正值）：
$$H\approx J^{T}J+\mu I$$
这也就得到了LM算法，将上述式子带入之前的公式，可以得到:
$$x_{k+1}=x_k?(J_k^T{J}_k+\mu I{)}^{?1}{g}_k$$
所以我们发现，当$\mu$接近于0时，这个算法近似于Gauss-Newton算法；当$\mu$很大时，这个算法近似于最速下降法。因此，这也是为什么LM算法称为Gauss-Newton算法与最速下降法的结合。用一张图表示几种算法之间的关系：