高德资讯

最优化方法6——线搜索算法

无约束优化问题是众多优化问题中的基本问题，它对于自变量的取值范围不加限制，因此可以不必考虑它的可行性。在众多无约束算法中，主要可以分为两类：线搜索算法和信赖域算法。而对于线搜索算法，根据搜索方向不同，可以被进一步分为梯度类算法，牛顿算法等。本节开始，对于线搜索算法和信赖域算法展开详细的介绍。

对于基本的无约束优化问题:

$\\min_{x\\in\\mathbb{R}^n}\\,f(x),\\quad (\\#)\\\\$

我们之前分析过，这个问题可以被近似的视为一个探索问题。即一个探险家从一个点 $x$ 处，此时的高度为 $f(x)$ 。如何到达山谷的最低点？此时他要做两件事：首先，下一步该往哪走；其次，选定方向后需要走多远停下以便重新更换方向。以上的两件事情被确定后，便可以一直重复，知道到达 $f(x)$ 的最小值点。

以上便是线搜索类方法的具象化描述。它的数学表述为：
给定当前的一个点 $x^k$ ，首先通过某种算法选取向量 $d^k$ ，之后确定一个正数 $\\alpha_k$ ，则可以到达下一个点为：

$x^{k+1}=x^k+\\alpha_kd^k,\\\\$

这里的 $d^k$ 被称为点 $x^k$ 处的搜索方向，而 $\\alpha_k$ 为相应的方向。这里要求

$(d^k)^\ op\ abla f(x^k)<0,\\\\$

即 $d^k$ 是一个下降方向，这样才可以保证了 $f(x)$ 的值会沿着我们预设的路径减少。线搜索的过程实际上就是一个迭代过程。如以上的探索问题所述，线搜索算法的两个重要步骤是：如何让选取方向 $d^k$ 和合适的步长 $\\alpha_k$ 。

本节首先回答第二个问题。引文尽管选取方向的方法有很多种，但是确定补偿的方法却十分的相似。
首先构造辅助函数：

$\\phi(\\alpha)=f(x^k+\\alpha d^k),\\\\$

其中 $d^k$ 是已经选定的下降方向， $\\alpha>0$ 。这个辅助函数表示：目标函数 $f(x)$ 在射线 $\\{x^k+\\alpha d^k:\\alpha>0\\}$ 上的限制。

线搜索的目标是选取合适的 $\\alpha_k$ 使得 $\\phi(\\alpha_k)$ 尽可能减小。但这一工作并不容易，因为如果步长取得过大，则容易跳过最优点，而如果步长过小，则进行计算得时间将会被拉长。我们需要权衡这两个方面，一个自然的想法是寻找 $\\alpha_k$ 使得

$\\alpha_k=\\arg\\min_{\\alpha>0}\\phi(\\alpha),\\\\$

这种线搜索算法被称为是精确的。类似的，如果我们不要求 $\\alpha_k$ 是 $\\phi$ 得最优值点，则此时的线搜索算法被称为是非精确的。精确线搜索算法往往会需要很大的计算量，因此，我们一般青睐于非精确线搜索算法。

在非精确线搜索算法中，选取 $\\alpha_k$ 需要满足一定的要求，这些要求被称为线搜索准则．这里指出，线搜索准则的合适与否直接决定了算法的收敛性，若选取不合适的线搜索准则将会导致算法无法收敛。如下图所示，左图表示步长过大，右图则是步长太小。

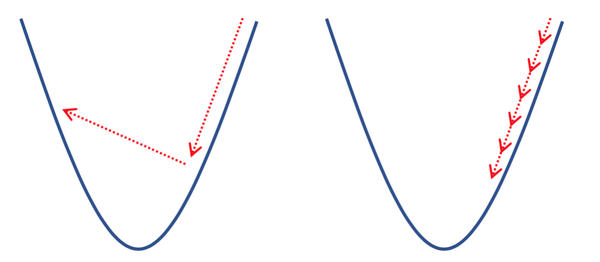
如我们考虑一个二次函数的优化问题， $\\min_xf(x)=x^2$ 。取初始点为 $x=1$ ，此时的方向只有两种选择 $\\{-1,+1\\}$ 。取 $d^k=-\\mathrm{sign}(x^k)$ ，考虑以下两种步长:

$\\alpha_{k,1}=\\frac{1}{3^{k+1}},\\quad \\alpha_{k,2}=1+\\frac{2}{3^{k+1}},\\\\$

不难计算得到

$x_1^k=\\frac{1}{2}\\left(1+\\frac{1}{3^k}\\right),\\quad x_2^k=\\frac{(-1)^k}{2}\\left(1+\\frac{1}{3^k}\\right),\\\\$

但是很明显，序列 $\\{x_1^k\\}$ 的极限并不是极小值点，序列 $\\{x_2^k\\}$ 根本不收敛。出现这种情况的原因是在迭代过程中函数值 $f(x^k)$ 的下降量不够充分，以至于算法无法收敛到极小值点．为了避免这种情况发生，必须引入一些更合理的线搜索准则来确保迭代的收敛性.

Armijo准则是一个常用的线搜索准则，它保证了每一步的迭代都是充分下降的。

Def 6.1： 设 $d^k$ 是点 $x^k$ 处的下降方向，如果对于常数 $c_1\\in(0,1)$ ，
$f(x^k+\\alpha d^k)\\leq f(x^k)+c_1\\alpha\ abla f(x^k)^\ op d^k,\\\\$
则称步长 $\\alpha$ 满足Armijo准则。

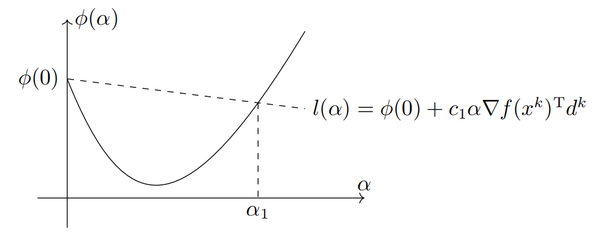
Armijo准则的几何意义如下图所示，点 $(\\alpha,\\phi(\\alpha))$ 必须在直线

$l(\\alpha)=\\phi(0)+c_1\\alpha\ abla f(x^k)^\ op d^k,\\\\$

的下方。则图中区间 $[0,\\alpha_1]$ 中的点都满足Armijo准则。由于 $d^k$ 是下降方向，即直线 $l(\\alpha)$ 的斜率为负。一般取 $c_1$ 为一个很小的正数。

但是仅仅使用Armijo准则并不能保证迭代的收敛性，这是因为 $\\alpha=0$ 显然满足条件，而这意味着迭代序列中的点固定不变，研究这样的步长是没有意义的。因此Armijo准则需要配合其他准则共同使用。

在优化算法的实现中，寻找一个满足Armijo准则的步长是比较容易的，一个最常用的算法是回退法。具体来说，回退法选取

$\\alpha_k=\\gamma^{j_0}\\hat{\\alpha},\\\\$

其中

$j_o=\\min\\{j=0,1,\\cdots|f(x^k+\\gamma^{j_0}\\hat{\\alpha}d^k)\\leq f(x^k)+c_1\\gamma^{j_0}\\hat{\\alpha}\ abla f(x^k)^\ op d^k\\},\\\\$

参数 $\\gamma\\in(0,1)$ 是一个给定的实数。

该算法被称为回退法是因为 $\\alpha$ 的试验值是由大至小的，它可以确保输出的 $\\alpha_k$ 能尽量地大．此外算法不会无限进行下去，因为 $d^k$ 是一个下降方向，当 $\\alpha_k$ 充分小时，Armijo准则总是成立的。

为了克服Armijo准则的缺陷，我们需要引入其他准则来保证每一步的 $\\alpha_k$ 不会太小．既然Armijo准则只要求点 $(\\alpha,\\phi(\\alpha))$ 必须处在某直线下方，我们也可使用相同的形式使得该点必须处在另一条直线的上方．这就是Armijo-Goldstein准则，简称Goldstein准则。

Def 6.2： 设 $d^k$ 是点 $x^k$ 处的下降方向，如果对于常数 $c\\in(0,\\frac{1}{2})$ ，
$\\begin{aligned}&f(x^k+\\alpha d^k)\\leq f(x^k)+c\\alpha\ abla f(x^k)^\ op d^k,\\\\ &f(x^k+\\alpha d^k)\\geq f(x^k)+(1-c)\\alpha\ abla f(x^k)^\ op d^k,\\end{aligned}\\\\$
则称步长 $\\alpha$ 满足Goldstein准则。

Goldstein 准则也有非常直观的几何含义，它指的是点 $(\\alpha,\\phi(\\alpha))$ 必须在两条直线

$\\begin{aligned}&l_1(\\alpha)=\\phi(0)+c\\alpha\ abla f(x^k)^\ op d^k,\\\\ &l_2(\\alpha)=\\phi(0)+(1-c)\\alpha\ abla f(x^k)^\ op d^k,\\end{aligned}\\\\$

之间．如下图所示，区间 $[\\alpha_1,\\alpha_2]$ 中的点均满足Goldstein准则．同时我们也注意到Goldstein准则确实去掉了过小的 $\\alpha$ 。

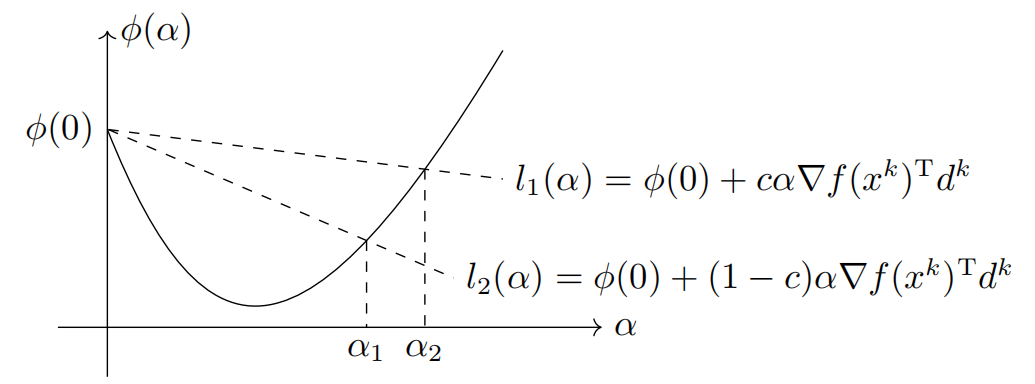
Goldstein 准则能够使得函数值充分下降，但是它可能避开了最优的函数值．如上图所示，一维函数 $\\phi(\\alpha)$ 的最小值点并不在满足 Goldstein 准则的区间 $[\\alpha_1,\\alpha_2]$ 中．为此我们引入 Armijo-Wolfe 准则，简称Wolfe准则.

Def 6.3： 设 $d^k$ 是点 $x^k$ 处的下降方向，如果对于常数 $c_1,c_2\\in(0,1)$ 且 $c_1<c_2$ ，
$\\begin{aligned}&f(x^k+\\alpha d^k)\\leq f(x^k)+c_1\\alpha\ abla f(x^k)^\ op d^k,\\\\ &\ abla f(x^k+\\alpha d^k)^\ op d^k\\geq c_2\ abla f(x^k)^\ op d^k,\\end{aligned}\\\\$
则称步长 $\\alpha$ 满足Wolfe准则。

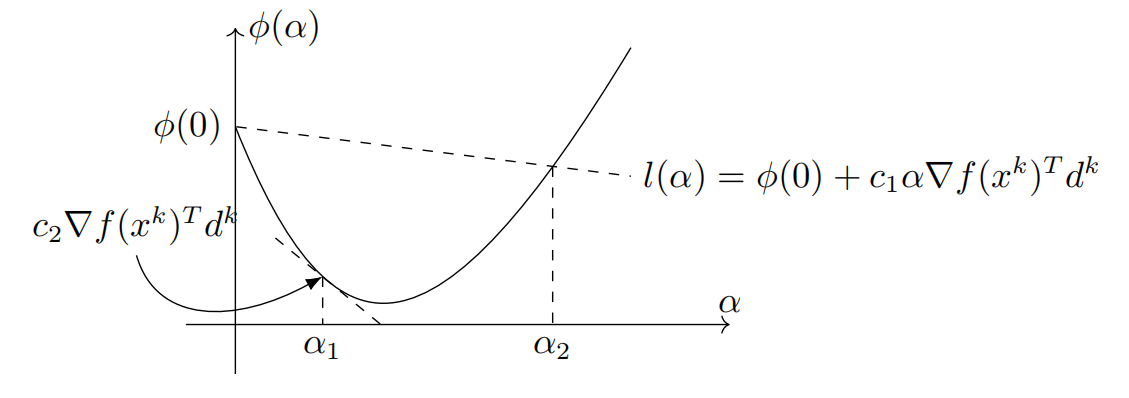
在准则(6.1.4)中，第一个不等式即是 Armijo 准则，而第二个不等式则是 Wolfe 准则的本质要求．注意到 $\ abla f(x^k+\\alpha d^k)^\ op d^k$ 恰好就是 $\\phi(\\alpha)$ 的导数，Wolfe 准则实际要求 $\\phi(\\alpha)$ 在点 $\\alpha$ 处切线的斜率不能小于 $\\phi'(0)$ 的 $c2$ 倍．如下图所示，在区间 $[\\alpha_1,\\alpha_2]$ 中的点均满足 Wolfe 准则。

注意到在 $\\phi(\\alpha)$ 的极小值点 $\\alpha^*$ 处有 $\\phi'(\\alpha^*)=f(x^k+\\alpha^* d^k)^\ op d^k$ ，因此 $\\alpha^*$ 永远满足Wolfe准则的第二个条件。而选择较小的 $c_1$ 可使得 $\\alpha^*$ 同时满足第一个条件，即 Wolfe 准则在绝大多数情况下会包含线搜索子问题的精确解。

以上介绍的三种准则都有一个共同点：使用这些准则产生的迭代点列都是单调的．在实际应用中，非单调算法有时会有更好的效果．这就需要我们应用非单调线搜索准则，这里介绍其中两种．

Def 6.4： 设 $d^k$ 是点 $x^k$ 处的下降方向， $M>0$ 为给定的正整数，如果
$f(x^k+\\alpha d^k)\\leq \\max_{0\\leq j\\leq\\min\\{k,M\\}}f(x^{k-j})+c_1\\alpha\ abla f(x^k)^\ op d^k,\\\\$
则称步长 $\\alpha$ 满足Grippo准则，其中 $c_1\\in (0,1)$ 为给定的常数。

Grippo准则和Armijo准则非常相似，区别在于Armijo准则要求下一次迭代的函数值 $f(x^{k+1})$ 相对于本次迭代的函数值 $f(x^k)$ 有充分下降，而Grippo准则只需要下一步函数值相比前面至多 $M$ 步以内迭代的函数值有下降就可以了。显然这一准则的要求比 Armijo准则更宽，它也不要求 $f(x^k)$ 的单调性。

Def 6.5： 设 $d^k$ 是点 $x^k$ 处的下降方向，如果
$f(x^k+\\alpha d^k)\\leq C^k+c_1\\alpha\ abla f(x^k)^\ op d^k,\\\\$
称步长 $\\alpha$ 满足Zhang-Hager准则，其中 $C^k$ 满足递推式 $C^0=f(x^0)$ ， $C^{k+1}=\\frac{1}{Q^{k+1}}(\\eta Q^kC^k+f(x^{k+1}))$ ，序列 $\\{Q^k\\}$ 满足 $Q^0=1$ ， $Q^{k+1}=\\eta Q^k+1$ ，参数 $\\eta,c_1\\in(0,1)$ 。

我们可以用以下的方式理解这个准则：变量 $C^k$ 实际上是本次搜索准则的参照函数值，即充分下降性质的起始标准；而下一步的标准 $C^{k+1}$ 则是函数值 $f(x^{k+1})$ 和 $C^k$ 的凸组合，并非仅仅依赖于 $f(x^{k+1})$ ，而凸组合的两个系数由参数 $\\eta$ 决定．可以看到当 $\\eta=0$ 时，此准则就是 Armijo 准则。

之前的讨论已经初步介绍了回退法，并指出该算法可以用于寻找 Armijo 准则的步长。实际上只要修改一下算法的终止条件，回退法就可以被用在其他线搜索准则之上，例如之前我们提到的两种非单调线搜索准则。
回退法的实现简单、原理直观，所以它是最常用的线搜索算法之一．然而，回退法的缺点也很明显：第一，它无法保证找到满足 Wolfe 准则的步长，但对一些优化算法而言，找到满足 Wolfe 准则的步长是十分必要的；第二，回退法以指数的方式缩小步长，因此对初值 $\\hat{\\alpha}$ 和参数 $\\gamma$ 的选取比较敏感，当 $\\gamma$ 过大时每一步试探步长改变量很小，此时回退法效率比较低，当 $\\gamma$ 过小时回退法过于激进，导致最终找到的步长太小，错过了选取大步长的机会。

为了提高回退法的效率，我们有基于多项式插值的线搜索算法．假设初始步长 $\\hat{\\alpha}_0$ 已给定，如果经过验证， $\\hat{\\alpha}_0$ 不满足 Armijo 准则，下一步就需要减小试探步长．和回退法不同，我们不直接将 $\\hat{\\alpha}_0$ 缩小常数倍，而是基于 $\\phi(0)$ ， $\\phi'(0)$ ， $\\phi(\\hat{\\alpha}_0)$ 这三个信息构造一个二次插值函数 $p_2(\\alpha)$ ，即寻找二次函数 $p_2(\\alpha)$ 满足

$p_2(0)=\\phi(0),\\quad p_2'(0)=\\phi'(0),\\quad p_2(\\hat{\\alpha}_0)=\\phi(\\hat{\\alpha}_0).\\\\$

以上三个条件可以唯一决定 $p_2(\\alpha)$ ，而且不难验证 $p_2(\\alpha)$ 的最小值点恰好位于 $(0,\\hat{\\alpha}_0)$ 内．此时取 $p_2(\\alpha)$ 的最小值点 $\\hat{\\alpha}_1$ 作为下一个试探点，利用同样的方式不断递归下去直至找到满足 Armijo 准则的点。

这一小节给出使用不同线搜索准则导出的算法的收敛性．此收敛性建立在一般的线搜索类算法的框架上。

Thm 6.6： 考虑一般的迭代格式
$x^{k+1}=x^k+\\alpha_k d^k,\\\\$
其中 $d^k$ 是搜索分析， $\\alpha_k$ 是步长，且在迭代过程中满足Wolfe准则。假设目标函数 $f$ 下有界，连续可微和梯度 $L$ -利普西茨连续性，即
$\\|\ abla f(x)-\ abla f(y)\\|\\leq L\\|x-y\\|,\\quad \\forall x,y\\in\\mathbb{R}^n,\\\\$
则
$\\sum_{k=0}^\\infty\\cos^2\ heta_k\\|\ abla f(x^k)\\|^2<+\\infty,\\\\$
其中 $\\cos\ heta_k$ 为负梯度 $-\ abla f(x^k)$ 和下降方向 $d^k$ 的夹角余弦，即
$\\cos\ heta_k=\\frac{-\ abla f(x^k)^\ op d^k}{\\|-\ abla f(x^k)^\ op\\|\\|d^k\\|},\\\\$
称为Zoutendijk条件。

Proof： 根据Wolfe准则的条件，有

$\\left(\ abla f(x^{x+1})-\ abla f(x^k)\\right)^\ op d^k\\geq(c_2-1)\ abla f(x^k)^\ op d^k,\\\\$

根据Cauchy不等式和梯度 $L$ -利普西茨连续性，有

$\\left(\ abla f(x^{x+1})-\ abla f(x^k)\\right)^\ op d^k\\leq\\|\ abla f(x^{x+1})-\ abla f(x^k)\\|\\|d^k\\|\\leq \\alpha_kL\\|d^k\\|,\\\\$

结合以上两个式子

$\\alpha_k\\geq \\frac{c_2-1}{L}\\frac{\ abla f(x^k)^\ op d^k}{\\|d^k\\|^2},\\\\$

由于 $\ abla f(x^k)^\ op d^k<0$ ，代入Wolfe条件，

$f(x^{k+1})\\leq f(x^k)+c_1\\frac{c_2-1}{L}\\frac{(\ abla f(x^k)^\ op d^k)^2}{\\|d^k\\|^2},\\\\$

这等价于

$f(x^{k+1})\\leq f(x^k)+c_1\\frac{c_2-1}{L}\\cos^2\ heta_k\\|\ abla f(x^k)\\|^2,\\\\$

再关于 $k$ 求和，我们有

$f(x^{k+1})\\leq f(x^k)-c_1\\frac{1-c_2}{L}\\sum_{j=0}^k\\cos^2\ heta_k\\|\ abla f(x^j)\\|^2,\\\\$

由于函数是下有界的，且由 $0<c_1<c_2<1$ 可知 $c_1(1-c_2)>0$ ，因此当 $k\ o\\infty$ 时，

$\\sum_{j=0}^\\infty\\cos^2\ heta_j\\|\ abla f(x^j)\\|^2<+\\infty,\\\\$

得证。 $\\blacksquare$

定理 6.1 指出，只要迭代点满足 Wolfe 准则，对梯度利普希茨连续且下有界函数总能推出Zoutendijk条件式成立．实际上采用Goldstein 准则也可推出类似的条件．Zoutendijk 定理刻画了线搜索准则的性质，配合下降方向 $d^k$ 的选取方式我们可以得到最基本的收敛性。

Prop 6.7： 对于一般的迭代格式
$x^{k+1}=x^k+\\alpha_k d^k,\\\\$
$\\cos\ heta_k$ 为负梯度 $-\ abla f(x^k)$ 和下降方向 $d^k$ 的夹角，并假设对于任意的 $k$ ，存在常数 $\\gamma>0$ ，使得
$\ heta_k<\\frac{\\pi}{2}-\\gamma,\\\\$
则在Zoutendijk定理成立的条件下，有
$\\lim_{k\ o\\infty}\ abla f(x^k)=0.\\\\$

Proof： 假设结论不成立，则存在子列 $\\{k_l\\}$ 和正常数 $\\delta>0$ ，使得

$\\|\ abla f(x^{k_l})\\|\\geq\\delta,\\quad l=1,2,\\cdots\\\\$

根据 $\ heta_k$ 的假设，对于任意的 $k$ ，有

$\\cos\ heta_k>\\sin\\gamma>0,$

仅考虑Zoutendijk条件的第 $k_l$ 项，有

$\\sum_{k=0}^\\infty\\cos^2\ heta_k\\|\ abla f(x^k)\\|^2\\geq\\sum_{l=0}^\\infty\\cos^2\ heta_{k_l}\\|\ abla f(x^{k_l})\\|^2\\geq\\sum_{l=1}^\\infty(\\sin^2\\gamma)\\delta^2\ o+\\infty,\\\\$

这和Zoutendijk定理矛盾。从而结论成立。 $\\blacksquare$

命题6.7建立在 Zoutendijk 条件之上，它的本质要求是Zoutendijk条件，即每一步的下降方向 $d^k$ 和负梯度方向不能趋于正交．这个条件的几何直观明显：当下降方向 $d^k$ 和梯度正交时，根据泰勒展开的一阶近似，目标函数值 $f(x^k)$ 几乎不发生改变．因此我们要求 $d^k$ 与梯度正交方向夹角有一致的下界．

命题6.7仅仅给出了最基本的收敛性，而没有更进一步回答算法的收敛速度．这是由于算法收敛速度极大地取决于 $d^k$ 的选取．接下来我们将着重介绍如何选取下降方向 $d^k$ 。

本文使用 Zhihu On VSCode 创作并发布

上一篇：抖音电商发布巨量千川跨境广告资质审核规范下一篇：商务部等10部门关于支持国家级经济技术开发区创新提升更好发挥示范作用若干措施的通知

栏目导航

高德资讯

联系我们

电话：13988888888

传真：海南省海口市

手机：0898-66889888

邮箱：88889999

地址：/public/upload/system/2018/07/28/2091301cca30ff8c6fd3ecd09c8d4b02.jpg

高德资讯

最优化方法6——线搜索算法

相关新闻

栏目导航

高德资讯

联系我们